接受-拒絕抽樣簡單來說就是使從樣本空間裡任意取出的樣本能符合所要求的機率分佈。
我們來考慮以下的問題:
給定一個樣本空間\(X\)和它的機率密度函數\(P(X)\),我們希望每一次從\(X\)中取出\(x_i\)時,其機率都能符合機率分佈\(P\),也就是\(P(x_i)\)。
這時問題來了,我們怎麼知道取出一個樣本的機率會符合想要的機率分佈?最常見的機率分佈之一是均勻分佈(uniform distribution)。當我們從\(X\)中取樣時,如果每個樣本的取樣機率都是一樣的,那麼該樣本空間就符合均勻分佈,這是很直覺的取樣方式,例如一個公正骰子擲出任一面的機率便是呈均勻分佈。而另一種常見的機率分佈是常態分佈(normal distribution),其樣本的機率分佈畫成圖時會呈鐘形。自然界中很多事物大體上呈常態分佈,如一個國家所有人民的身高體重。
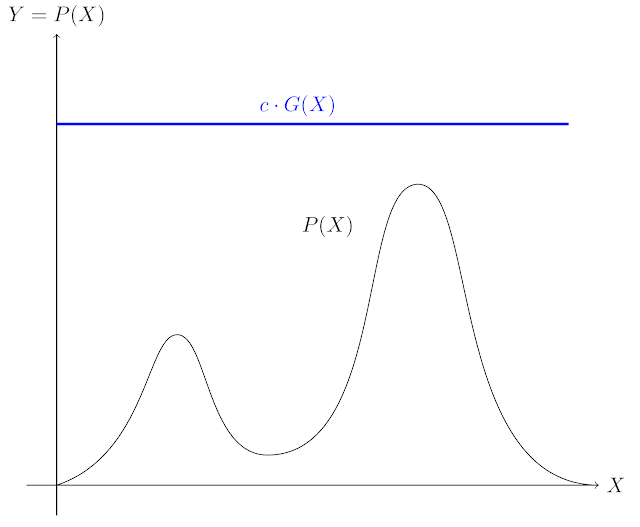
但如果機率分佈不是以上提到的兩種,而且取出的樣本數很少的時候,我們就很難確定取出的樣本是否符合指定的機率分佈了。在這裡我們來考慮下面這個任意的機率密度函數\(P(X)\):
我們希望在\(X\)中任意取出的\(x_i\)能滿足\(P\),但要怎麼做呢?首先,我們先畫一條水平線\(G(X)\),很明顯它是均勻分佈的圖形,如果它不在\(P(X)\)的上方,那麼就乘上一個常數\(c\)使它位於\(P(X)\)上方:
在最理想的狀況下,我們希望水平線和\(P(X)\)最高點相切。
接下來我們要對\(X\)進行取樣,程序如下:
- 在\(X\)中任取一個樣本\(x_i\)
- 令\(u\)為\([0,1]\)中的任意值,也就是說\(u\sim U(0,1)\)
- 如果\(u\leq P(x_i)/(c\cdot G(x_i))\),則接受\(x_i\)為符合\(P(X)\)的樣本
這個取樣程序是很簡單的,但為何這樣會對呢?我們先在\(P(X)\)上任取兩點,並令他們到\(X\)軸的距離為\(\ell_1, \ell_2\):
在程序中\(P(x_i)/(c\cdot G(x_i))\)愈大,\(u\leq P(x_i)/(c\cdot G(x_i))\)愈容易成立,就有愈大的機率能使得\(x_i\)被取樣。而\(c\cdot G(x_i)\)是固定的,所以樣本是否容易被取出就是由\(P(x_i)\)來決定。在圖中\(\ell_2>\ell_1\),所以\(x_2\)相對於\(x_1\)更容易被取樣。
由於我們每次是根據均勻分佈來取\(x_i\),再由上述程序決定它是否符合\(P(X)\),因此我們令
\[Pr(X)=G(X),\]
而給定一個樣本判斷它是否符合\(P(X)\)的機率為
\[Pr(accept|X)=\frac{P(X)}{c\cdot G(X)},\]
另可得
\[Pr(accept)=\int_{x_i} Pr(accept|x_i)\cdot Pr(x_i)dx_i=\int_{x_i}\frac{P(x_i)}{c\cdot G(x_i)}G(x_i)dx_i=\frac{1}{c},\]
根據貝氏定理,我們可以得到
\[Pr(X|accept)=\frac{Pr(accept|X)Pr(X)}{Pr(accept)}=\frac{\frac{P(X)}{c\cdot G(X)}G(X)}{\frac{1}{c}}=P(X),\]
也就是說我們希望在機率分佈\(P(X)\)被滿足的狀況下所取出能被接受的\(x_i\)會符合\(P(X)\)。
這個方法也有缺點,首先這只適用於單變數的機率密度函數,而且如果只有少部份的樣本機率較高,其他大部份樣本的機率低的話,就不容易取到樣本了。
參考資料:
Acceptance-Rejection Sampling
圖形的LaTeX code:
\begin{tikzpicture}[scale=0.5]
%\draw[style=help lines] (-1,-1) grid[step=1cm] (18,14);
\draw[->] (-1,0) to (18,0) node[right] {$X$};
\draw[->] (0,-1) to (0,15) node[above] {$Y=P(X)$};
\draw (0,0) .. controls (3,1) and (3,5) .. (4,5)
.. controls (5,5) and (5,1) .. (7,1)
.. controls (11,1) and (10,10) .. (12,10)
.. controls (14,10) and (13,0) .. (18,0);
\draw (9,8) node[above] {$P(X)$};
\draw[blue, style=very thick] (0,12) to (17,12);
\draw[blue] (8,12) node[above] {$c\cdot G(X)$};
\draw[red, style=very thick, <->] (4,0) to (4,5);
\draw (4,3) node[left] {$\ell_1$};
\draw (4,5) node[above] {$x_1$};
\draw[red, style=very thick, <->] (12,0) to (12,10);
\draw (12,5) node[left] {$\ell_2$};
\draw (12,10) node[above] {$x_2$};
\end{tikzpicture}