今天考完了客語中高級測驗後,再次體認到,即使是自以為從小在家聽到大的客語,也無法臨時抱佛腳來考,也再次證明語言考試永遠是我的罩門,也不得不承認語言這種事是無法速成的。早上筆試結束時,聽到幾位大姐討論題目,便加入她們,才知道原來就算是從小說客語長大的母語人士,也不容易準備中高級測驗;本來沒有文字的客語加上另外制定出來的音標和文字,造出一套似乎可以檢知一個人客語整合聽說讀寫能力的測驗。
客語是一個以聽和說為主要用途的語言,其能力便是建立在發音的基礎上。可以想見如果發音不清楚,那麼聽的人也不容易聽懂講的人在說什麼。母語人士學習發音的方式是直接模仿發音,所以英美人士也不太需要用音標來學英語發音;而非母語人士需要藉由一個中介方式輔助學習,例如我們需要用KK音標、DJ音標或萬國音標來學習英語發音,或是使用IPA國際音標。因此母語人士考客語檢定的第一個困難就是儘管很多字詞都會講,但寫成音標(類似河洛語白話字POJ系統,教育部有制定台灣客家語拼音方案,符號基本上參考漢音拼音)時,幾乎大多數都看不懂,因為沒有受過聲韻學或發音訓練的人,是無法看懂拼音符號的(不過學過韓語或越南語的人還是能看懂同樣發音方式的ptk/bdg語尾)。以這種方式來測驗母語人士的程度,實在有待商榷。音標不是不能用,只是它的用途應是給毫無基礎的人一個學習發音的方式。
另外一方面,文字也不是客語在日常生活中會經常存在的元素。儘管客委會邀集許多在聲韻學、訓詁學、文字史方面學有專精的專家,經由多方考證後制定出一套客語的文字,但畢竟用客語書寫的機會實在少之又少,這些生澀冷僻的文字很容易就被人束之高閣。我不認為這些文字的存在是不應該的,但若是要拿來成為一套測試語言能力的標準,我想大家可以再討論看看要怎麼做比較好。社會大眾對於客語文字的接受度仍然偏低,且日常生活中河洛文字的用量仍然佔大多數,也為較多人所接受。客語文字的推行仍然有一段路要走。
但對我來說,客語推行至今令人最感欣慰的是,客委會的四縣腔教材終於加註美濃腔調的發音方式。雖然使用四縣腔的人口佔全國客家人的六成以上,台鐵、高鐵、北高捷運的系統也都以四縣腔為客語廣播的使用腔調,南部六堆的四縣腔卻是佔少數的。而美濃雖屬六堆,但客語部份的發音又和六堆客語略有不同。儘管學習四縣腔並不困難,六堆四縣腔的學習資源亦不難取得,但以文化傳承的角度來看,若未將美濃音特別標出,美濃客家人後代若要學習自己家鄉的腔調或做文史考證時,將會遇到極大困難。他們可能學到的客家話,已經不是他們父母親、叔叔伯伯、姑姑阿姨、阿公阿媽、外公外婆所說的客家話了。因此我認為新版教材標註美濃音是對美濃客家族群的尊重,也是一大進步。
話說回來,這個測驗本來的用意是要測驗考生本身是否能流利且嫻熟地使用客語,並進一步了解客家文化。語言和文化本來就是一體的。通過中高級認證者,將有機會進一步獲得教授客語或薪傳教師資格。就考試領導學習的角度來看,這個測驗不啻是一個鼓勵民眾學習客語,並對客家文化更加關心的動力。就文化永續保存的角度來看,也具有十分正面的效益。儘管很多方面需要改進和討論,但總體來說,從2005年開辦初級認證、2008年開辦中級暨中高級認證至今,行政院客委會在推動客家政策方面的努力是看得見的,並且一直在進步當中。我樂見這些改變,並樂觀期待母語在台灣能夠永續保存下去。
2013年12月29日 星期日
2013年2月14日 星期四
Scatter plot 散點圖的繪製
在資料分析時,我們可能需要畫散點圖(scatter plot)來表示某一組數據的分佈狀況。在\(\LaTeX\)裡,使用TikZ就能達到這個目的。
先看以下語法
\documentclass{article}
\usepackage{tikz}
\begin{document}
\begin{tikzpicture}[only marks]
\draw plot[mark=*, mark size=.3] file {data};
\end{tikzpicture}
\end{document}
先看以下語法
\documentclass{article}
\usepackage{tikz}
\begin{document}
\begin{tikzpicture}[only marks]
\draw plot[mark=*, mark size=.3] file {data};
\end{tikzpicture}
\end{document}
plot後面的mark代表繪圖要用的圖案,有*, +, x等可以選擇,mark size是圖案的大小。file後面接著的是儲存要畫出來的所有點的座標的檔名,檔案內容為:
0.10503 -0.47536
-0.087392 0.093255
0.055823 -0.29088
0.17298 -0.17674
0.1019 0.09943
...
在此只列出前五個點的座標,而我存了一千個點,要注意的圖案大小過大的話,點就不能畫太多,會出現錯誤訊息。在這個例子裡,我使用以下的MATLAB指令來產生點的位置:
.3.*randn(1000,2)
這個指令產生1000個點,每個點的x和y座標值都是來自標準常態分佈,再乘以0.3。
產生結果如下:
2013年2月12日 星期二
單變數抽樣 - Acceptance-Rejection Sampling 接受-拒絕抽樣
接受-拒絕抽樣簡單來說就是使從樣本空間裡任意取出的樣本能符合所要求的機率分佈。
我們來考慮以下的問題:
給定一個樣本空間\(X\)和它的機率密度函數\(P(X)\),我們希望每一次從\(X\)中取出\(x_i\)時,其機率都能符合機率分佈\(P\),也就是\(P(x_i)\)。
這時問題來了,我們怎麼知道取出一個樣本的機率會符合想要的機率分佈?最常見的機率分佈之一是均勻分佈(uniform distribution)。當我們從\(X\)中取樣時,如果每個樣本的取樣機率都是一樣的,那麼該樣本空間就符合均勻分佈,這是很直覺的取樣方式,例如一個公正骰子擲出任一面的機率便是呈均勻分佈。而另一種常見的機率分佈是常態分佈(normal distribution),其樣本的機率分佈畫成圖時會呈鐘形。自然界中很多事物大體上呈常態分佈,如一個國家所有人民的身高體重。
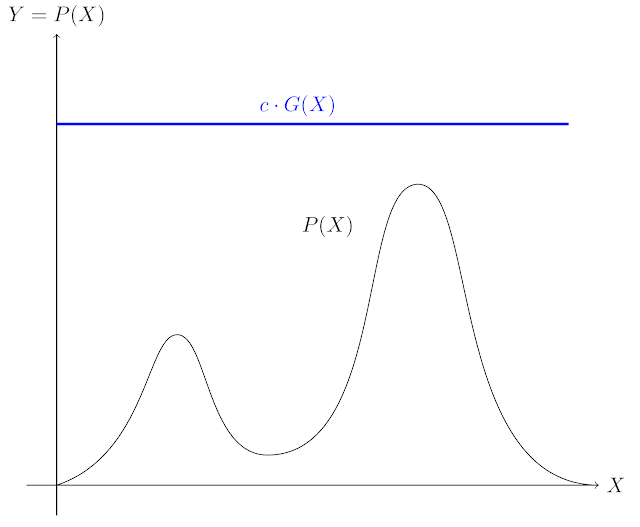
但如果機率分佈不是以上提到的兩種,而且取出的樣本數很少的時候,我們就很難確定取出的樣本是否符合指定的機率分佈了。在這裡我們來考慮下面這個任意的機率密度函數\(P(X)\):
我們希望在\(X\)中任意取出的\(x_i\)能滿足\(P\),但要怎麼做呢?首先,我們先畫一條水平線\(G(X)\),很明顯它是均勻分佈的圖形,如果它不在\(P(X)\)的上方,那麼就乘上一個常數\(c\)使它位於\(P(X)\)上方:
在最理想的狀況下,我們希望水平線和\(P(X)\)最高點相切。
接下來我們要對\(X\)進行取樣,程序如下:
- 在\(X\)中任取一個樣本\(x_i\)
- 令\(u\)為\([0,1]\)中的任意值,也就是說\(u\sim U(0,1)\)
- 如果\(u\leq P(x_i)/(c\cdot G(x_i))\),則接受\(x_i\)為符合\(P(X)\)的樣本
在程序中\(P(x_i)/(c\cdot G(x_i))\)愈大,\(u\leq P(x_i)/(c\cdot G(x_i))\)愈容易成立,就有愈大的機率能使得\(x_i\)被取樣。而\(c\cdot G(x_i)\)是固定的,所以樣本是否容易被取出就是由\(P(x_i)\)來決定。在圖中\(\ell_2>\ell_1\),所以\(x_2\)相對於\(x_1\)更容易被取樣。
由於我們每次是根據均勻分佈來取\(x_i\),再由上述程序決定它是否符合\(P(X)\),因此我們令
\[Pr(X)=G(X),\]
而給定一個樣本判斷它是否符合\(P(X)\)的機率為
\[Pr(accept|X)=\frac{P(X)}{c\cdot G(X)},\]
另可得
\[Pr(accept)=\int_{x_i} Pr(accept|x_i)\cdot Pr(x_i)dx_i=\int_{x_i}\frac{P(x_i)}{c\cdot G(x_i)}G(x_i)dx_i=\frac{1}{c},\]
根據貝氏定理,我們可以得到
\[Pr(X|accept)=\frac{Pr(accept|X)Pr(X)}{Pr(accept)}=\frac{\frac{P(X)}{c\cdot G(X)}G(X)}{\frac{1}{c}}=P(X),\]
也就是說我們希望在機率分佈\(P(X)\)被滿足的狀況下所取出能被接受的\(x_i\)會符合\(P(X)\)。
這個方法也有缺點,首先這只適用於單變數的機率密度函數,而且如果只有少部份的樣本機率較高,其他大部份樣本的機率低的話,就不容易取到樣本了。
參考資料:
Acceptance-Rejection Sampling
圖形的LaTeX code:
\begin{tikzpicture}[scale=0.5]
%\draw[style=help lines] (-1,-1) grid[step=1cm] (18,14);
\draw[->] (-1,0) to (18,0) node[right] {$X$};
\draw[->] (0,-1) to (0,15) node[above] {$Y=P(X)$};
\draw (0,0) .. controls (3,1) and (3,5) .. (4,5)
.. controls (5,5) and (5,1) .. (7,1)
.. controls (11,1) and (10,10) .. (12,10)
.. controls (14,10) and (13,0) .. (18,0);
\draw (9,8) node[above] {$P(X)$};
\draw[blue, style=very thick] (0,12) to (17,12);
\draw[blue] (8,12) node[above] {$c\cdot G(X)$};
\draw[red, style=very thick, <->] (4,0) to (4,5);
\draw (4,3) node[left] {$\ell_1$};
\draw (4,5) node[above] {$x_1$};
\draw[red, style=very thick, <->] (12,0) to (12,10);
\draw (12,5) node[left] {$\ell_2$};
\draw (12,10) node[above] {$x_2$};
\end{tikzpicture}
這個方法也有缺點,首先這只適用於單變數的機率密度函數,而且如果只有少部份的樣本機率較高,其他大部份樣本的機率低的話,就不容易取到樣本了。
參考資料:
Acceptance-Rejection Sampling
圖形的LaTeX code:
\begin{tikzpicture}[scale=0.5]
%\draw[style=help lines] (-1,-1) grid[step=1cm] (18,14);
\draw[->] (-1,0) to (18,0) node[right] {$X$};
\draw[->] (0,-1) to (0,15) node[above] {$Y=P(X)$};
\draw (0,0) .. controls (3,1) and (3,5) .. (4,5)
.. controls (5,5) and (5,1) .. (7,1)
.. controls (11,1) and (10,10) .. (12,10)
.. controls (14,10) and (13,0) .. (18,0);
\draw (9,8) node[above] {$P(X)$};
\draw[blue, style=very thick] (0,12) to (17,12);
\draw[blue] (8,12) node[above] {$c\cdot G(X)$};
\draw[red, style=very thick, <->] (4,0) to (4,5);
\draw (4,3) node[left] {$\ell_1$};
\draw (4,5) node[above] {$x_1$};
\draw[red, style=very thick, <->] (12,0) to (12,10);
\draw (12,5) node[left] {$\ell_2$};
\draw (12,10) node[above] {$x_2$};
\end{tikzpicture}
訂閱:
意見 (Atom)